基础
基本原理
扩散模型
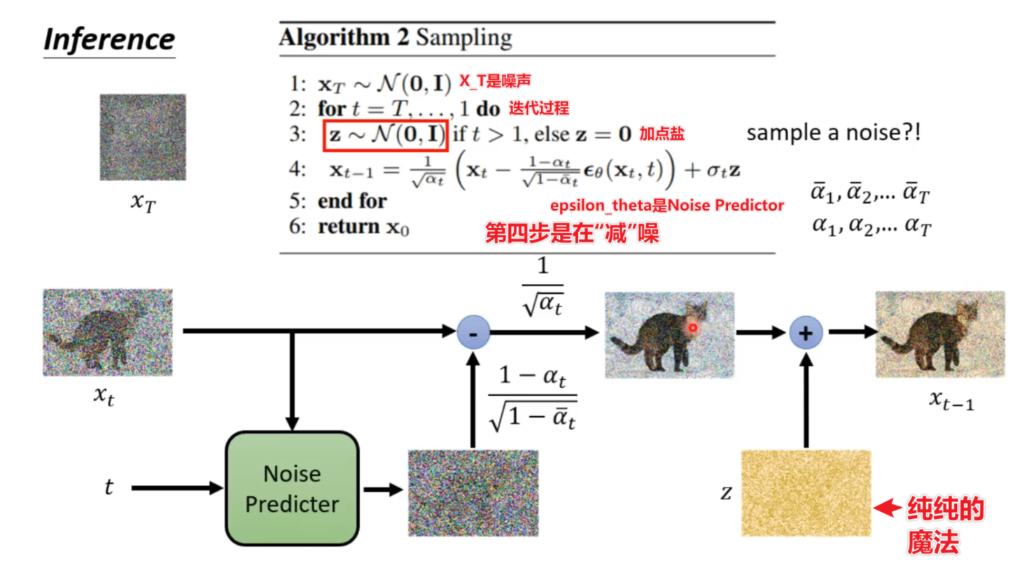
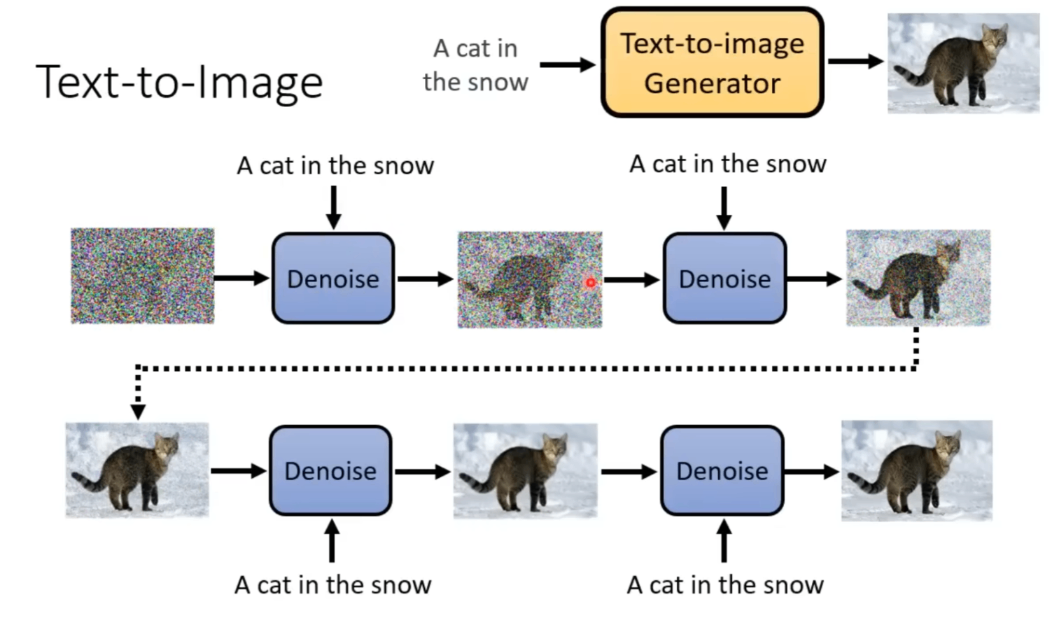
扩散模型是一个迭代式的方法,通过一步一步地对图片进行“降噪”来得到最终图片。流程如下
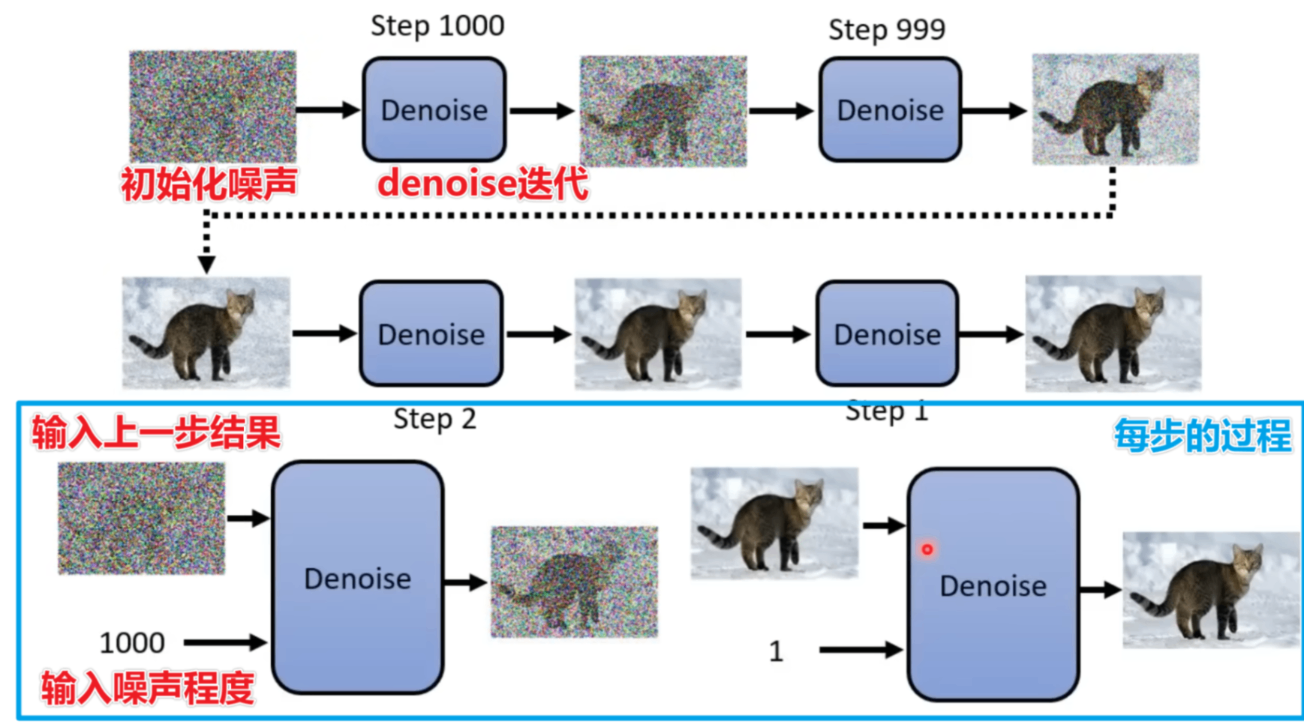 每次denoise的过程如下:
每次denoise的过程如下:
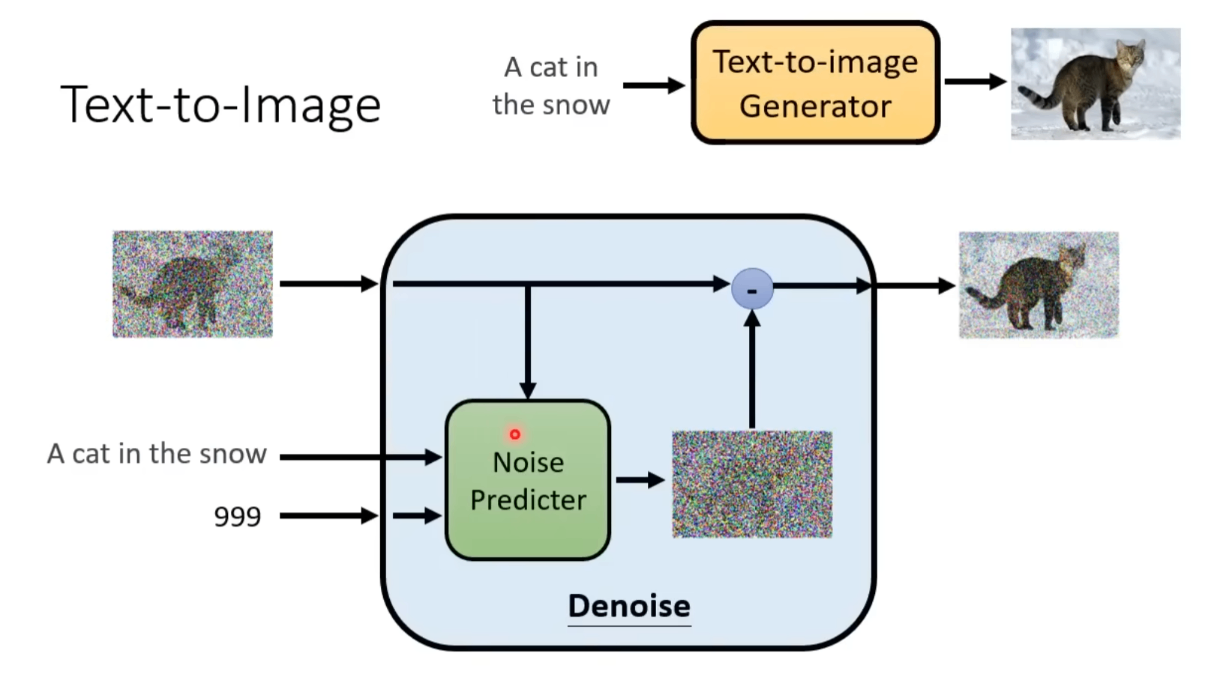
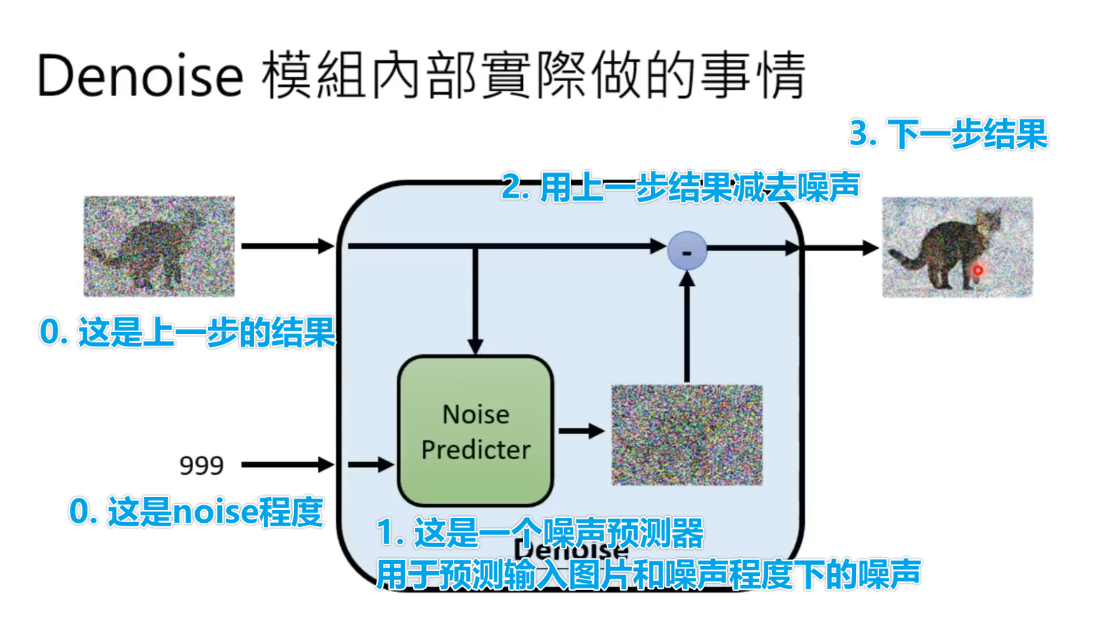 李宏毅认为,之所以不直接预测出不带noise的图片,是因为这样的方法比较难。直接生产噪声比较简单。
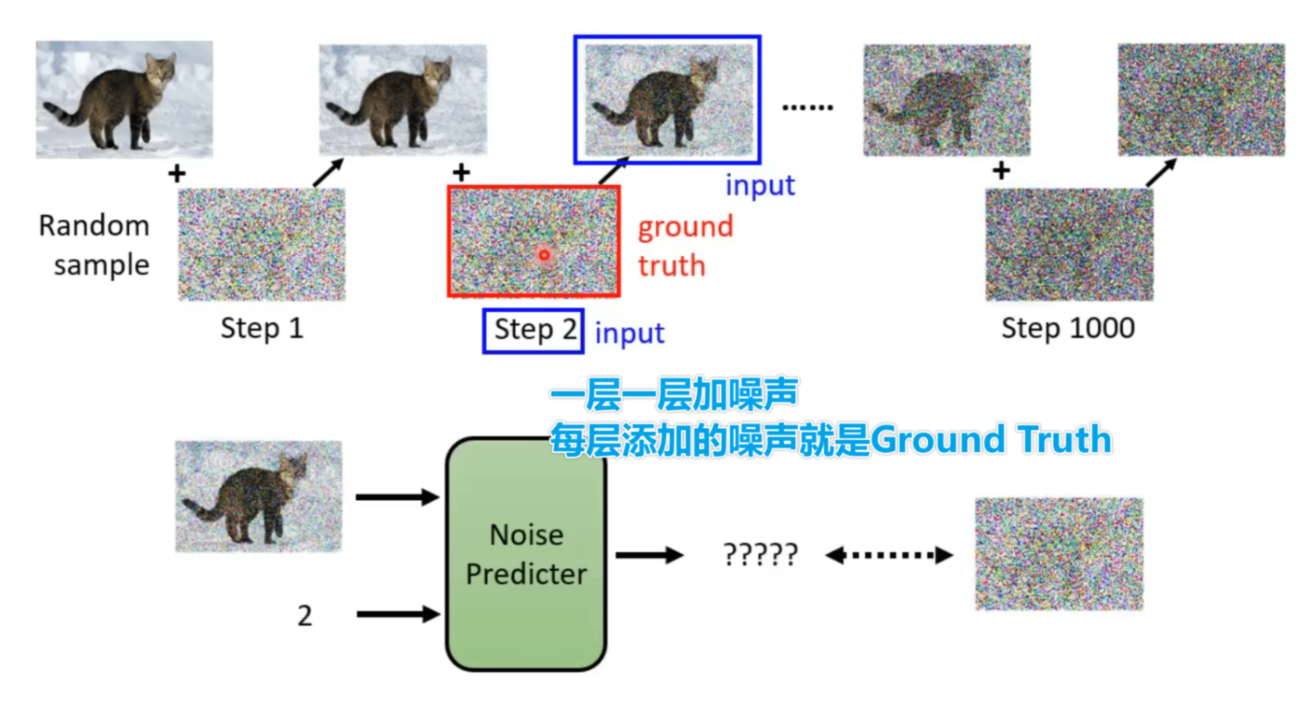
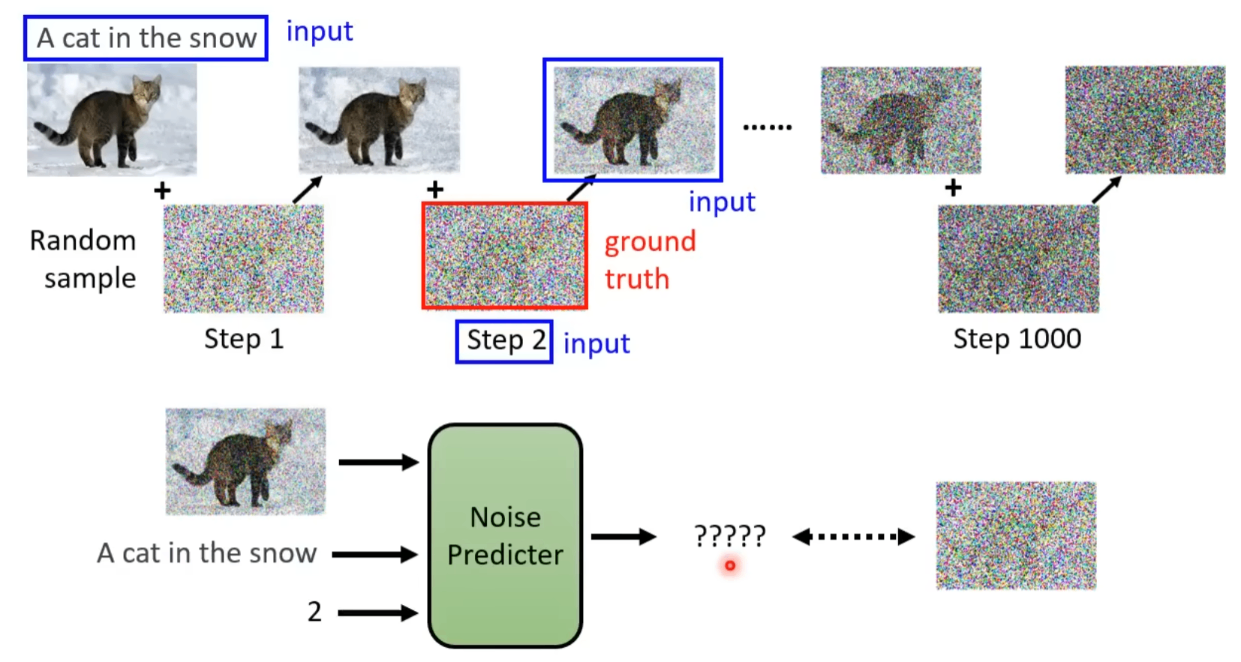
这个noise predicter的训练集是可以生成的,生成方法如下:
李宏毅认为,之所以不直接预测出不带noise的图片,是因为这样的方法比较难。直接生产噪声比较简单。
这个noise predicter的训练集是可以生成的,生成方法如下:
文生图
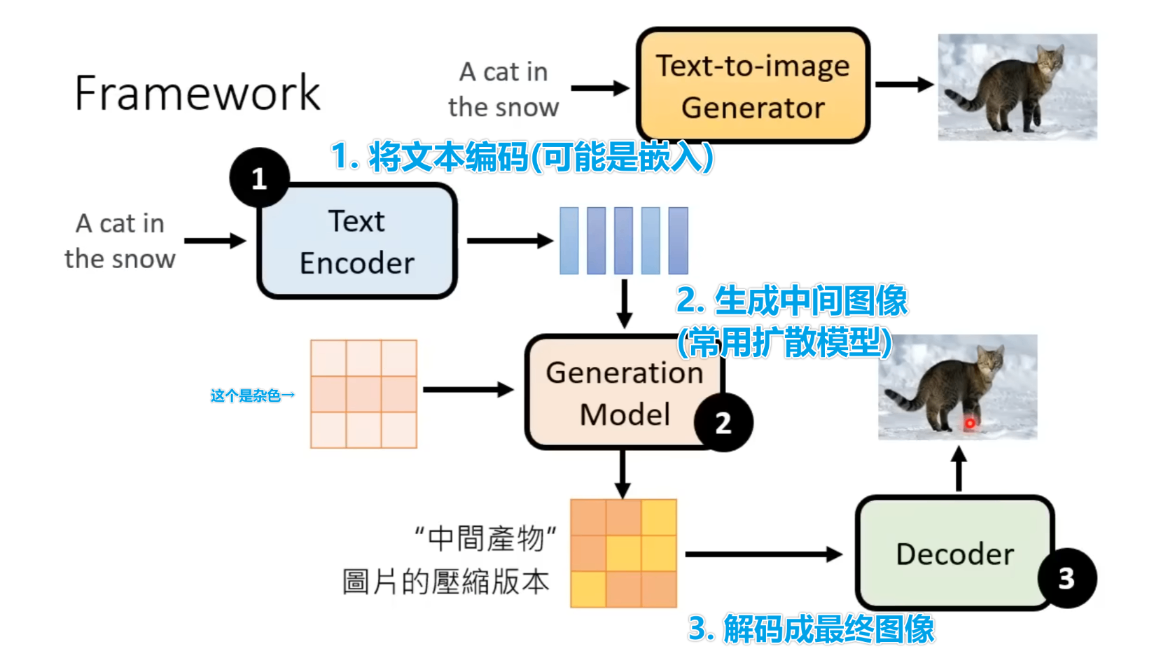
加入文字后的扩散模型,对应变成了如下几个过程:
 仅仅是加入了文字指示。
仅仅是加入了文字指示。
落地的文生图模型的一般方法
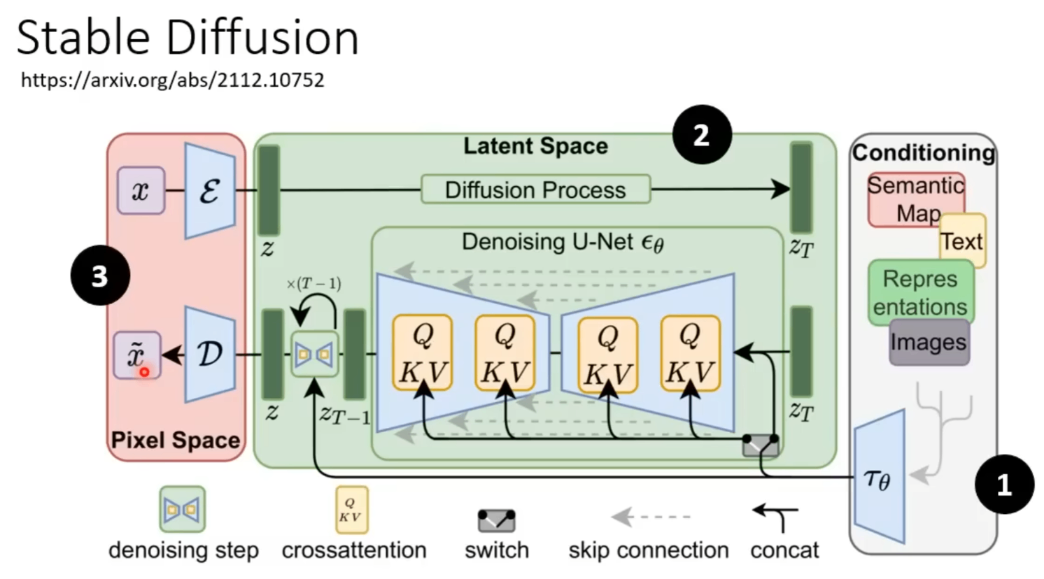
 例如stable diffusion就如下:
例如stable diffusion就如下:
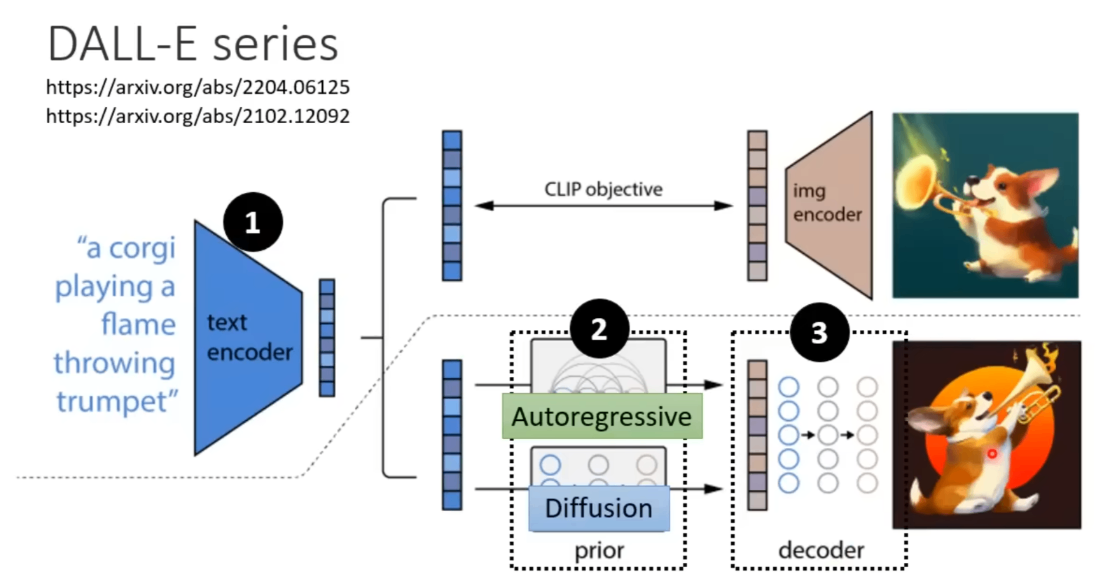
 DALL-E(至少是初代)也是这样:
DALL-E(至少是初代)也是这样:
各阶段使用的模型
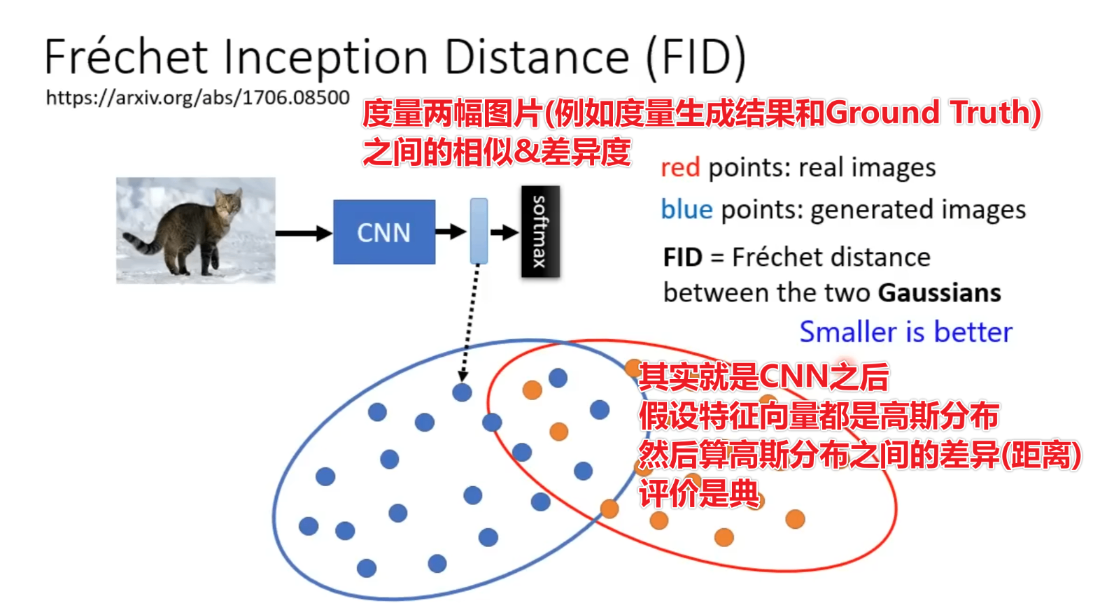
生成图像与Ground Truth之间的差别量化
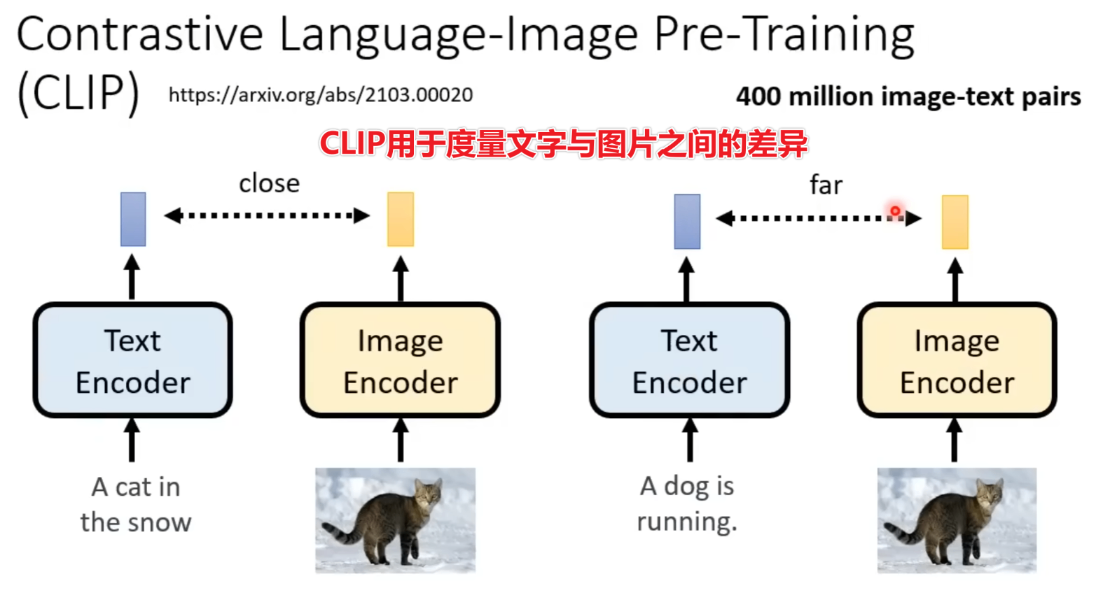
文字与图片的差异
Decoder
在进行完步骤2时,我们会得到中间结果,中间结果可能是一张结果图像的缩略图,也可能是一个Latent Representation,这时就需要用一个Decoder将其进行处理,得到最后的图像。
- 当中间结果是缩略图的时候,只需要训练一个upscale的模型就好了。
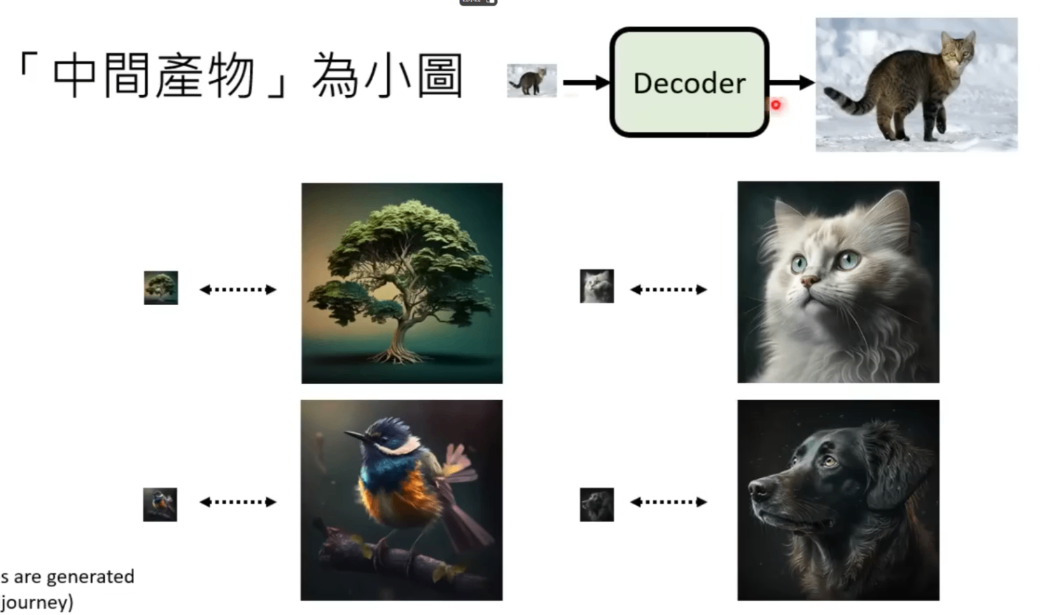
- 当中间结果是隐藏表示时,那你还需要训练一个Auto Encoder。
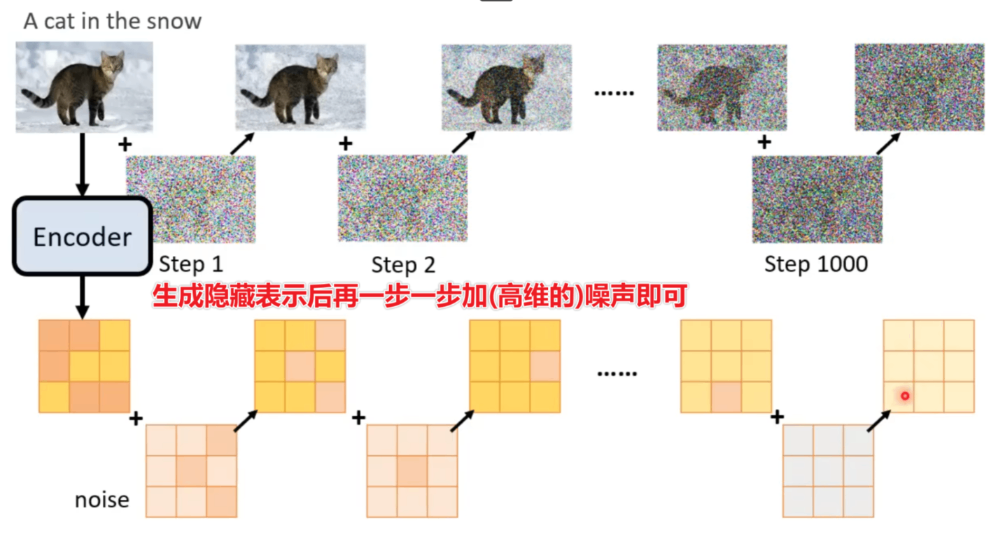
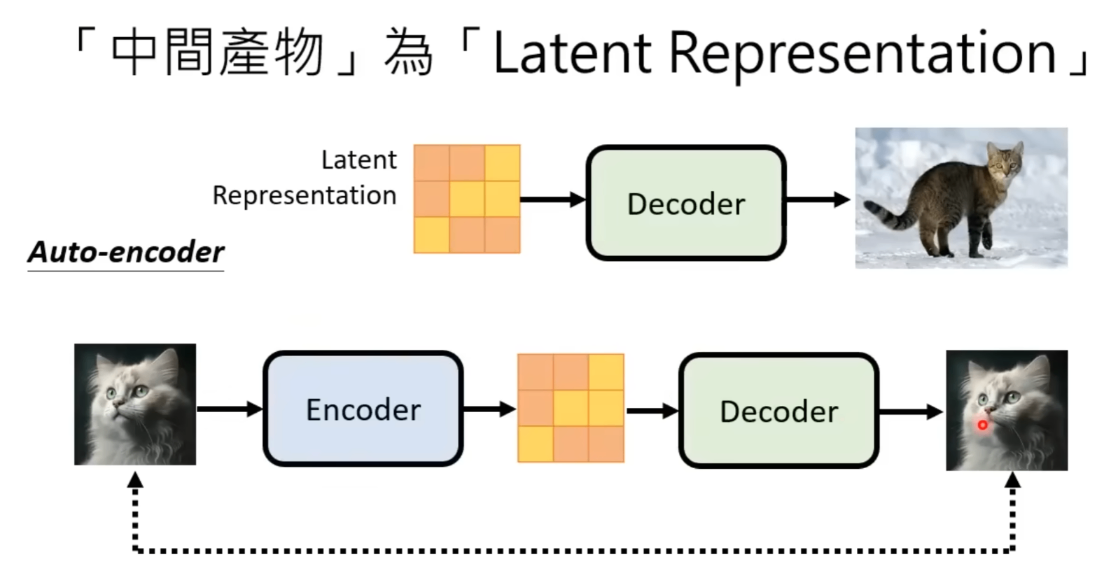 对于这种情况,训练扩散模型时也要进行对应的改动。下图是与之前模型的对比。
对于这种情况,训练扩散模型时也要进行对应的改动。下图是与之前模型的对比。
具体原理
建议查看[此篇文章](扩散模型 (Diffusion Model) 简要介绍与源码分析 (qq.com)),非常详细。
扩散模型
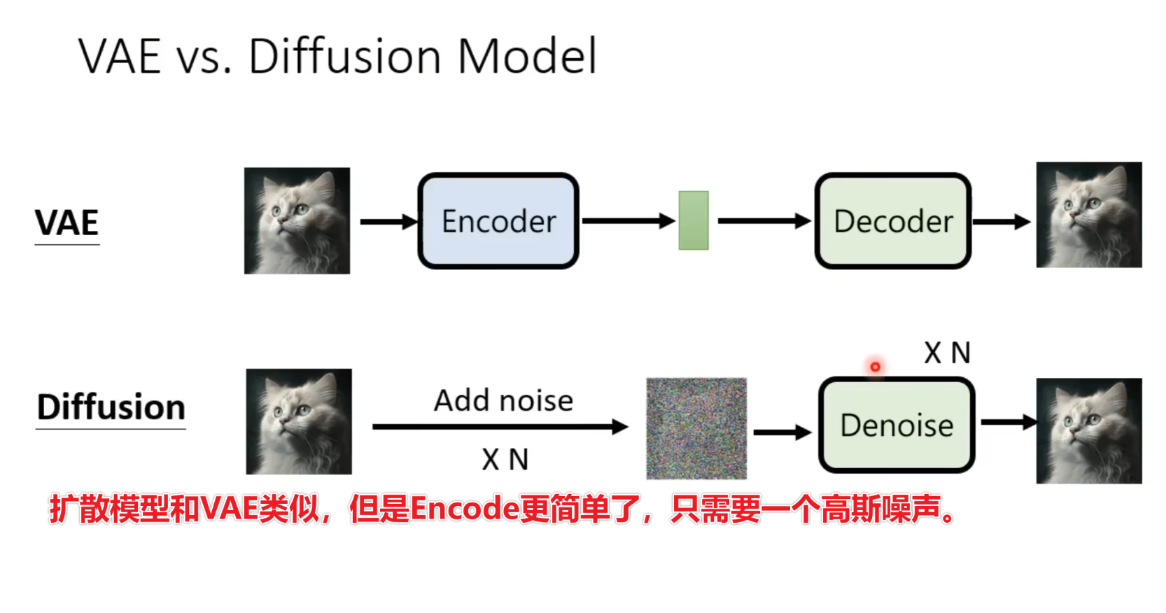
与VAE的对比
训练
前向过程
前向过程会将原图一步一步添加越来越弱的噪声,直到将图片变为完全噪声图。
我们考虑这个噪声添加过程一共分为T步,第t步时,第t步的加噪声后的图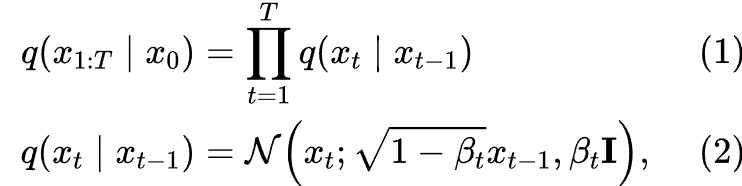 其中
其中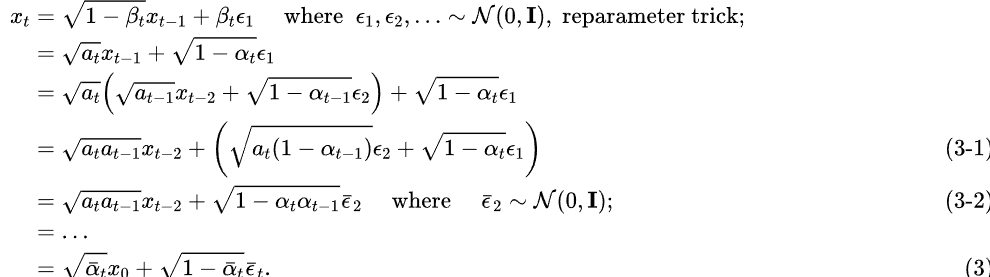 (3-1)和(3-2)的推导是由于独立高斯分布的可见性。把
(3-1)和(3-2)的推导是由于独立高斯分布的可见性。把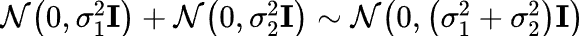 这也就是说,其实只需要一步就可以求出第t步的噪声图。
这也就是说,其实只需要一步就可以求出第t步的噪声图。
反向过程
反向过程是根据输入的带噪声的图像,预测出其中的噪声,然后再去除这个噪声即可得到不带噪声的图。本质上是获取逆向分布
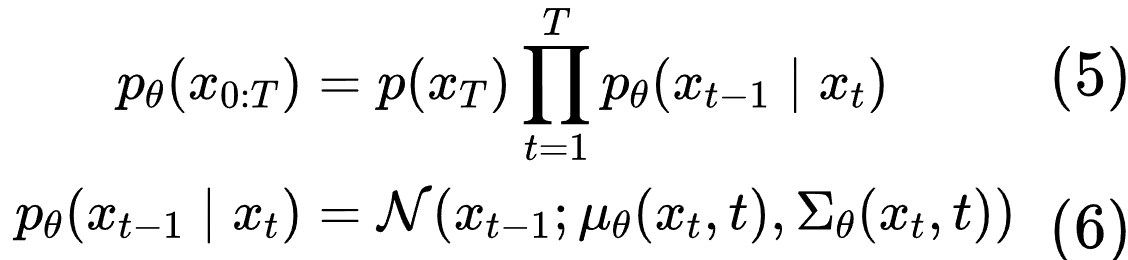 (5)很好理解,也是一个马尔可夫过程,所以分布是连乘的。
而(6)是我们要求的目标函数。
在知道
(5)很好理解,也是一个马尔可夫过程,所以分布是连乘的。
而(6)是我们要求的目标函数。
在知道 通过分离指数部分,可以求出方差和均值公式(8)(9)。
通过分离指数部分,可以求出方差和均值公式(8)(9)。
 可以得出如下的分布
可以得出如下的分布
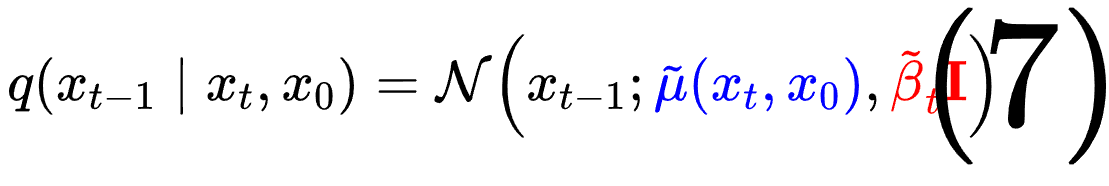 此外,前向过程中我们已经知道了
此外,前向过程中我们已经知道了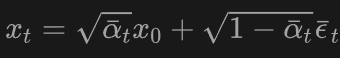 代入(9)中有
代入(9)中有
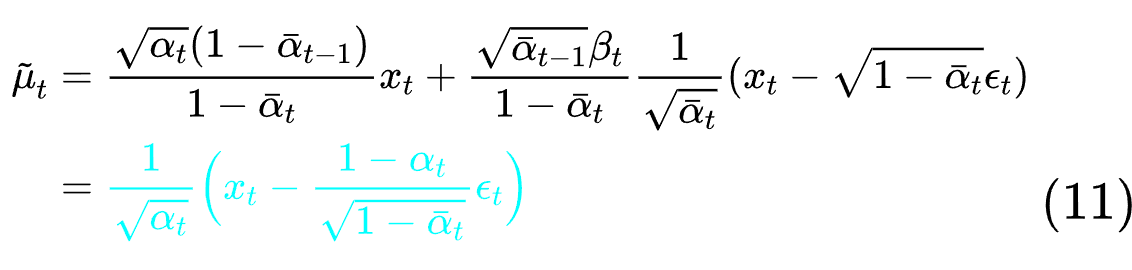 是个简单的代入过程。此时我们的
是个简单的代入过程。此时我们的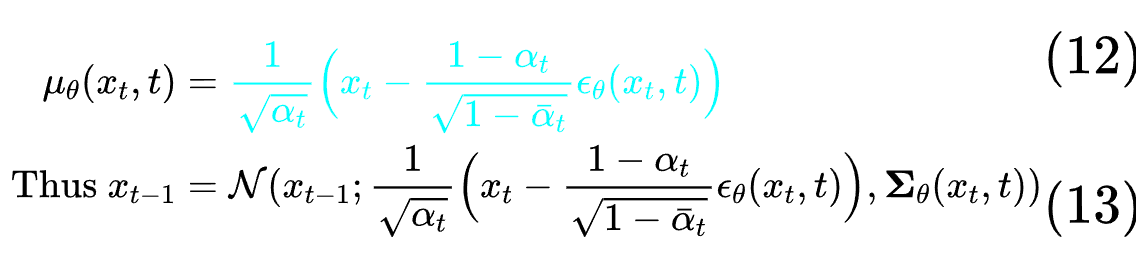 现在有了拟合的均值,(8)式中得到的方差公式中也没有未知数,也就是说方差是完全已知的。有了方差和拟合均值,正态分布也就可以进行拟合了。
现在有了拟合的均值,(8)式中得到的方差公式中也没有未知数,也就是说方差是完全已知的。有了方差和拟合均值,正态分布也就可以进行拟合了。
损失函数
我们知道第t步的噪声
模型的损失函数即为下图第5步的公式,也就是真实添加的噪声与预测噪声的距离。
 上图标错了,t越大α_t越小噪声越大。
神经网络+损失函数。至此我们完成了整个扩散模型。
上图标错了,t越大α_t越小噪声越大。
神经网络+损失函数。至此我们完成了整个扩散模型。
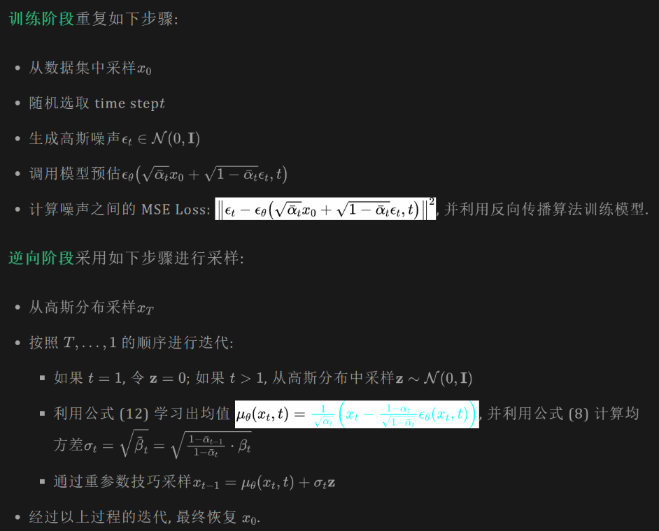
推理
推理其实就是没啥好说的了,就直接采样一个标准正态分布作为